The Mathematical Paradox That Lets You Create Something From Nothing

It was April 1989, and the International Gold Council in New York was on the warpath. The culprit: the late AK Dewdney, a mathematician and computer scientist at the University of Western Ontario – and the man who, in one recent column for Scientific American, had thrown into jeopardy the entire basis of global civilization.

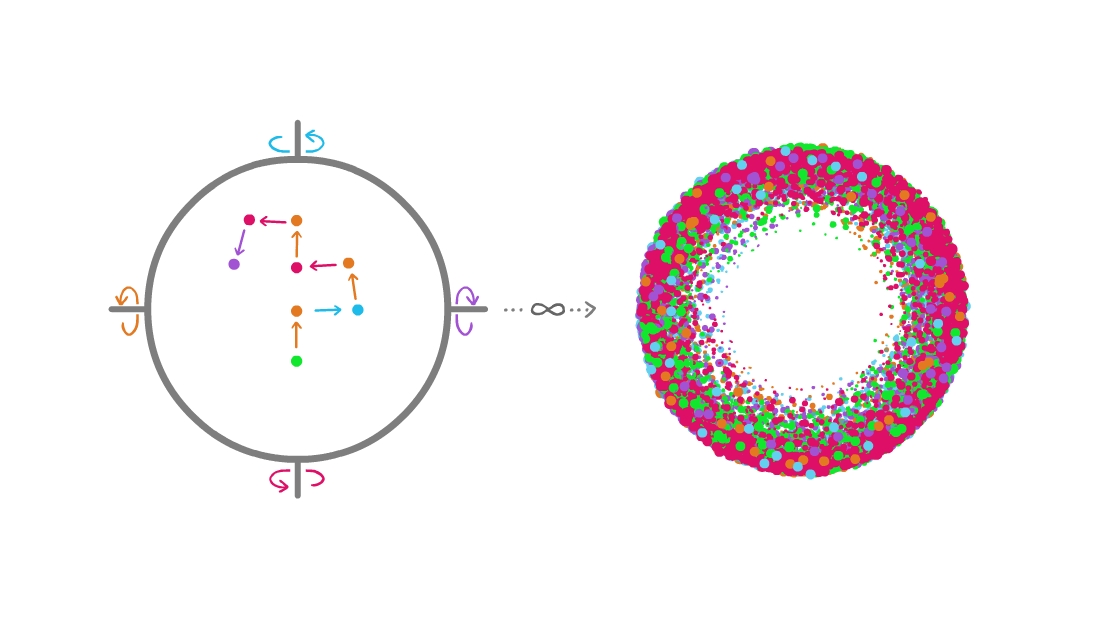
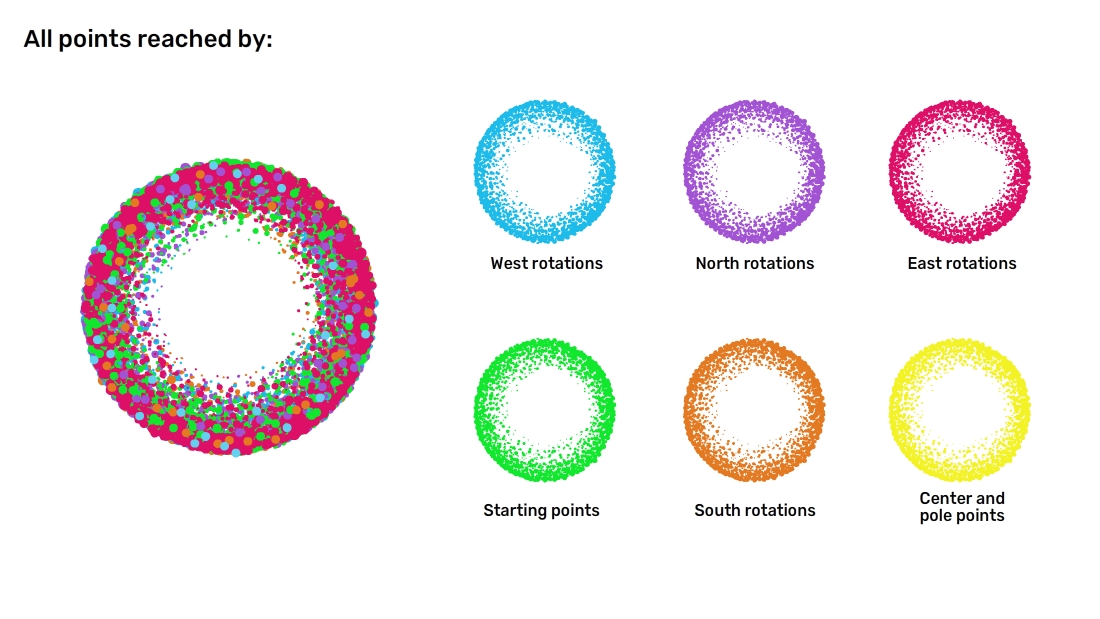
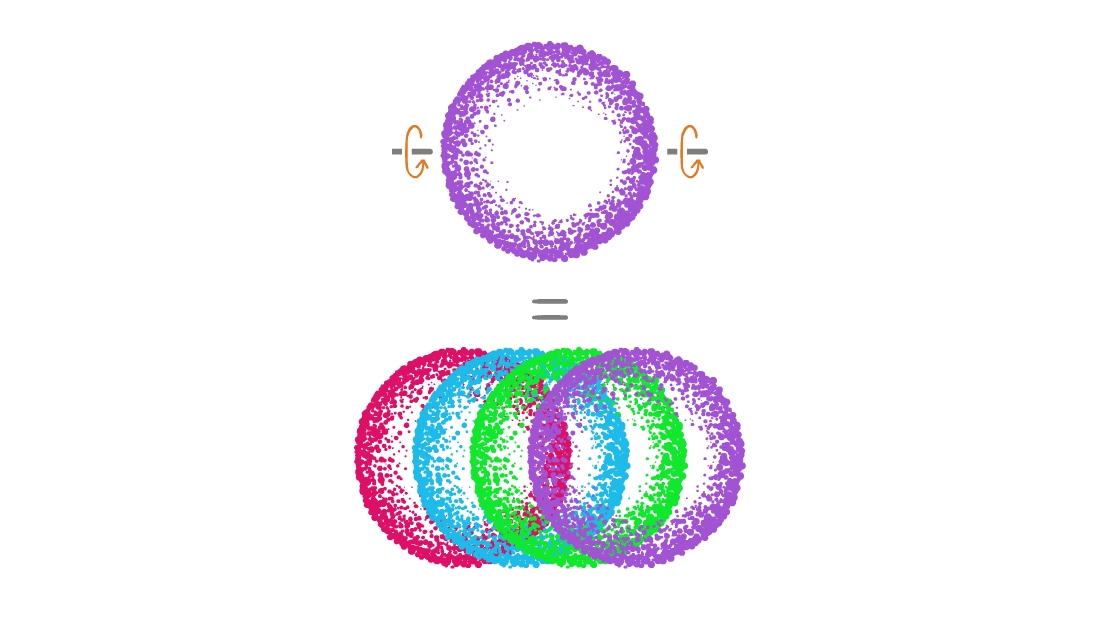
The rest of this article is behind a paywall. Please sign in or subscribe to access the full content.

How? By relating the results of his colleague, one Arlo Lipof, who had recently discovered a way to create gold out of thin air. “The inventor based his assertion on a legitimate mathematical result known as the Banach-Tarski Paradox,” Dewdney explained, which “reveals how under certain conditions an ideal solid can be cut into pieces and then reassembled into a new solid twice as large as the original one.”

In response, the Gold Council wrote in to the same magazine, warning of “turmoil” and the “collapse of civilization” that should be expected now that Lipof’s secret was out. “For years the IGC has made the Banach-Tarski paradox inaccessible to the general public,” they wrote. “We have always known that the apocalyptic reality of making more gold from less gold would have dire consequences for the international balance of world monetary systems.”

But could it be true? Is it really possible to take a solid, like a sphere, disassemble it into pieces, and then take those pieces and use them to build two spheres of the same size and volume and mass of the original? To literally create something from nothing?

Well, as the more skeptical among you may have intuited, the answer is “no” – at least, for the most part. “Arlo Lipof” never existed – the name is an anagram of “April fool” – and the Banach-Tarski paradox can’t be used to create gold from nothing. But apart from that… it’s pretty legit.

Have mathematicians lost their collective minds? Not quite. Here’s how it works.

An infinitely confusing proposition

Math is no stranger to confusing, unexpected results – but few are so straightforwardly, obviously, pants-on-fire-ly counterintuitive as the Banach-Tarski paradox. This is no “huh, that’s weird” kind of mindbender – the Banach-Tarski paradox almost flat-out states that 1 = 2.

“[The] Banach-Tarski Paradox […] seems patently impossible,” wrote Stan Wagon, Professor Emeritus in experimental mathematics at Macalester College, in his 2012 book on the paradox. “[It] is often stated as: It is possible to cut up a pea into finitely many pieces that can be rearranged to form a ball the size of the Sun!”

To come up with a result as weird as this, you need to be using some equally mind-bending math – and indeed, this paradox comes to us from the world of set theoretic geometry. If that’s not familiar to you, just know set theory is the field that gave us hundreds of pages of dense theoretical workings just to prove that 1 + 1 = 2. 

It’s also one of the bits of math that deals with infinities – and that’s going to be really important for understanding how the Banach-Tarski paradox works. 

“It has been known since antiquity that the notion of infinity leads very quickly to seemingly paradoxical constructions,” Wagon noted. “In a famous example, Galileo observed that the set of positive integers can be put into a one-one correspondence with the set of square integers, even though the set of nonsquares, and hence the set of all integers, seems more numerous than the squares.”

Got that? It’s a simple idea, though you may never have heard it put so succinctly: there are an infinite number of integers, and every one of them can be squared – meaning there are the same number of squares as there are integers. But, at the same time, obviously there are more integers than square integers. Just look at the span between zero and 10: 11 integers but only four squares.

It may seem like yet another paradox, but it’s really just an effect of dealing with infinities – the sets of both types of number are in fact the same size, and mathematicians call that size “countably infinite”. That name isn’t as oxymoronic as it sounds: it literally just means the numbers can be counted – or to use the mathematical terminology, put into a one-to-one correspondence with the set of natural numbers – not that a “final” member is necessarily going to be reached.

Contrasting with countably infinite sets are the uncountably infinite ones – sets whose members cannot be paired up with the natural numbers. The most obvious example is the set of real numbers: sure, you can start your list at zero, but what’s next? One? 0.1? 0.000001? There’s no way to know, because you can always get a little bit closer to zero.

The result of this is that uncountably infinite sets are infinitely larger than countably infinite sets – and if you need a second to let that sink in properly, feel free to take it, because it’s only going to get weirder from here. If you identify every point on and in a sphere with a real number – making it “solid” only really by virtue of being a collection of individual points that are so infinitely close to each other that no holes can possibly fit in there – then using these same arguments from set theory, you can actually decompose it into (deep breath) an uncountably infinite number of countably infinite sets. Simple, huh?

How to create something from nothing

These infinite sets aren’t arbitrary. To split the sphere, you’re first going to want to pick a point – anywhere in the sphere will do. Then, pick two angles – again, any will do, so long as they’re irrational – one for North-South rotations, and one for East-West rotations.

Then, it’s simply a case of picking a direction and rotating through the appropriate angle. You can go in any direction you like, for an infinite number of steps, with only one restriction: no backtracking over the step directly previous to the current one – no going North and then immediately South, for example.

Once you’ve done this an infinite number of times – and it will be countably infinite, since the rotations can be listed in the order you made them – you’ll have a set with that many points (and because we chose irrational angles, none will overlap). And if you do the same thing, over and over again, starting from every point on the sphere, then eventually you can create the uncountably infinite collection of countably infinite sets you were promised.

But we’re not finished yet! The next thing to do is to split these points up into six categories: those that were reached by a North rotation, those reached by a South rotation, those reached by East and West rotations, the starting points, and the center and pole points. Now, combined, these only make the one original sphere – but with a sneaky little trick, we can seemingly break the laws of physics.

Take one of the sets – let’s say, the one made from all the points reached by a North rotation – and negate the last move, in this case by rotating the points South. Now, remember, we only defined that group based on the very last step – meaning that now, all the points in the set came from different final rotations. In other words: we now have a set comprising all starting points, plus an infinite number of points whose most recent rotation was East, West, and crucially, North, which you may note is the very same group we started with. 

In other words: you can extract these three other groups out of the North rotation group, without losing any points from that set. Free duplicates!

Using the same idea, we can rotate the South rotation group to get the East, West, and South groups; the East group will give us the North, South, and East group; and the West group will give us the North, South, and West group. The poles and center point group need a slightly different finagling, but can also be duplicated through this infinite trickery.

Complete the right combination of these rotatory chicaneries, and you’ll eventually have an extra clone of all six groups. Combine these, and you have a duplicate of the original – you’ve doubled your sphere count and volume, all thanks to some mathematical machinations and a bit of set theory.

Some caveats

If all this sounds too good to be true – or at least, too confusing to be correct – then you’re not alone. Some mathematicians see its apparent absurdity as evidence of a mistake – that something’s gone awry with the foundations of math themselves, if these are the conclusions they can lead to.

And it should be pointed out that the Banach-Tarski paradox might be bunk. It only holds if we accept the Axiom of Choice, which is a complicated little technicality of math that can never be proven to be true or false – accepting it is essentially the closest math gets to religion.

In that respect, the Banach-Tarski paradox could be an argument for mathematical atheism – but to be honest, any controversy it once created has now mostly blown over. Belief in the Axiom of Choice is now pretty widespread – there are too many results that depend on it – and if we accept one, then we have to allow the other.

And sure, it may not grant the power to create gold from thin air – but that’s what we have the Curry Paradox for, isn’t it?